Smoothing
Smoothing is the process of removing noise from raw a input signal. Several techniques exist, from simple to more complicated. Smoothing methods are implemented by the Smoothing class. This class contains static methods for filtering signals directly, as well as methods for creating delegates that perform smoothing.
We will illustrate the different techniques using generated data:
int N = 200;
double scale = Constants.TwoPi / N;
var signal = Vector.FromFunction(N, i => Math.Sin(scale * i));
var noise = 0.1 * Vector.RandomNormal(N);
var y = signal + noise;
int windowLength = 21;Padding
Smoothing near the start and end of a signal can be challenging because fewer surrounding points are available. Many smoothers have the option of padding the data to obtain certain effects. The options are specified by a Padding value, which may take on the following values:
Value | Description |
|---|---|
None | The signal is not padded. Calculations are done using fewer values if necessary. |
Constant | The signal is padded with a constant value, which must be specified separately. |
Mirror | The values near the boundary are mirrored around the point on the boundary. |
Nearest | The signal is padded with the first value at the lower boundary and the last value at the upper boundary. |
Periodic | The signal is treated as periodic. The lower boundary is padded with values near the upper boundary, and vice versa. |
Moving average smoothing
The simplest way to remove noise is to take the simple mean or average. The MovingAverage(Vector<Double>, Int32, Padding, Double) method. This method takes up to 4 arguments. The first argument is a Vector<T> that contains the signal. The second argument is the window length. This is an integer that specifies the number of points that should be included in the average. It must be odd.
The third and fourth arguments are optional. They specify the padding to be applied, and, if constant padding is specified, the constant value. The method returns the smoothed signal. By default, no padding is used. In this case, fewer observations are used in the calculation of the smoothed signal near the boundaries.
The MovingAverageSmoother(Int32, Padding, Double) method returns a delegate that applies a moving average smoother with the specified window length.
In the code that follows, we compute the moving average of the signal. The chart below shows the result:
var yMA = Smoothing.MovingAverage(y, windowLength);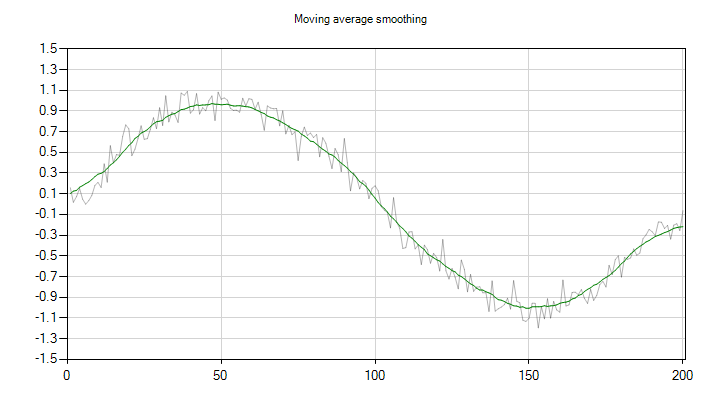
We can also look at the effect of padding. The code below computes the smoothed signal using mirrored and periodic padding. The chart below zooms into the left part of the signal to show the difference between the methods.
var yMirrored = Smoothing.MovingAverage(y, windowLength, padding: Padding.Mirror);
var yPeriodic = Smoothing.MovingAverage(y, windowLength, padding: Padding.Periodic);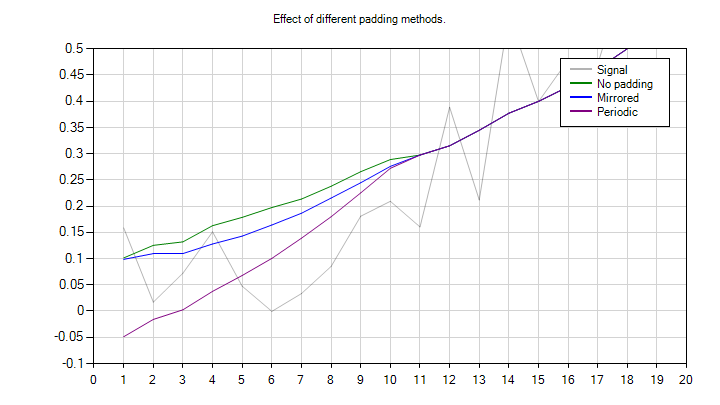
Savitsky-Golay smoothing
Savitsky-Golay smoothing is one of the most commonly used techniques for removing noise from a signal. It works by locally fitting a least squares polynomial and using the value of the fitted polynomial at the center point as the smoothed value. Savitsky-Golay filters allow the approximation of derivatives of the signal. The SavitskyGolay(Vector<Double>, Int32, Int32, Int32, Padding, Double) method. This method takes up to 6 arguments. The first argument is once again a Vector<T> that contains the signal. The second argument is an integer that specifies the number of points that should be included in the average. The third argument specifies the order or degree of the fitted polynomials.
The fourth argument specifies the order of the derivative that should be returned. The default value is 0, which means that the smoothed original series is returned. A value of 1 indicates the first derivative, and so on. The order must be less than or equal to the polynomial order of the filter. The fifth and sixth arguments are also optional. They specify the padding to be applied, and, if constant padding is specified, the constant value. The method returns the smoothed signal, or one of its derivatives.
By default, no padding is used. In this case, the polynomial fitted for the first or last full group of points is used to compute the smoothed values at the boundaries.
The SavitskyGolaySmoother(Int32, Int32, Int32, Padding, Double) method returns a delegate that applies a Savitsky-Golay smoother with the specified window length, polynomial order, and derivative order. The coefficients used to compute the smoothed values are pre-computed. If the same filter is applied to multiple signals, then using a smoother delegate will give considerably better performance.
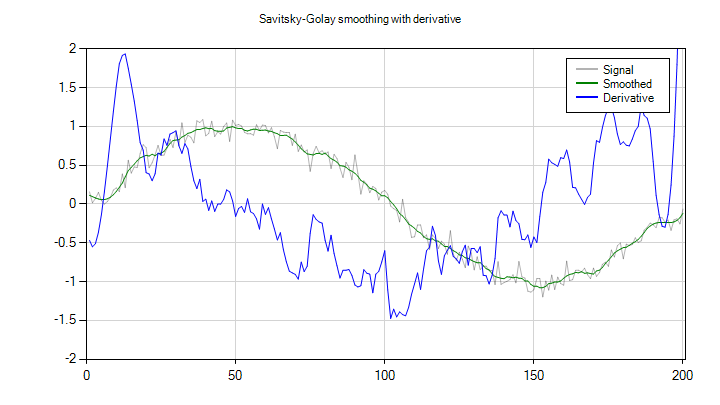
The code below applies the Savitsky-Golay smoother with a bandwidth of 21 and polynomial order 4. We also create a smoother that computes the smoothed first derivative using the same parameters. Finally, we apply this smoother to the signal to get an approximation to the first derivative, multiplied by a suitable scale factor:
var ySG = Smoothing.SavitskyGolay(y, windowLength, 4);
var sgSmoother = Smoothing.SavitskyGolaySmoother(windowLength, 4, 1);
var dySG = (1 / scale) * sgSmoother(y);The results are shown below. The derivative is still quite noisy, but also clearly shows the cosine shape we would expect.
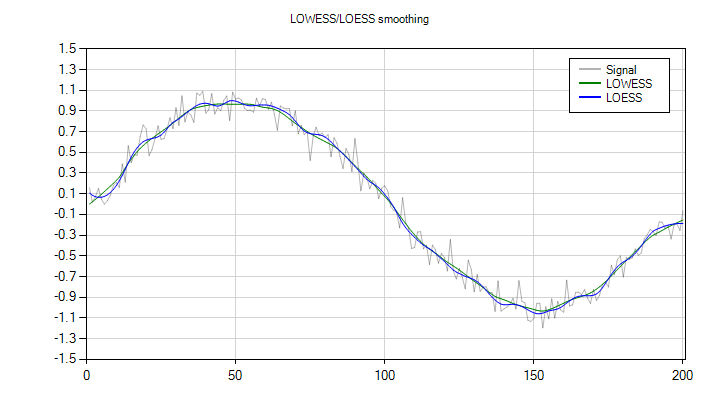
LOWESS and LOESS smoothing
LOWESS stands for LOcally WEighted Scatterplot Smoothing. It works by computing a regression line through the neighbourhood for each point. The points are weighted based on their distance to the central point. LOESS is a generalization to multiple dimensions and higher degree polynomials. Only one-dimensional LOESS is available. Optionally, a robust regression can be used by iteratively re-weighting each data point based on its residual.
The Lowess method computes the LOWESS smoothing using local linear regression, while Loess computes the LOESS smoothing using local quadratic polynomial regression. Both these methods take up to 5 arguments. The first argument is the Vector<T> that contains the signal. The second argument specifies the number of points that should be included in the average. It may be provided as an integer, or as a real number. In the latter case, the specifies the fraction of the total number of data points in the signal that should be used for the regression.
The third argument is optional. It specifies the number of robustness iterations should be performed. The default is 0. The fourth argument is also optional and specifies the width of a window where interpolation may be used instead of computing the full regression.
Loess smoothing can use data points that are not evenly spaced. In this case, the vector containing the x values should be supplied as the first argument, before all other arguments discussed earlier. The x values should be in ascending order. Duplicates are allowed.
The LowessSmoother and LoessSmoother methods return a delegate that applies the LOWESS and LOESS algorithms, respectively, to its argument using the specified window length and robustness iterations. The LowessScatterSmoother and LoessScatterSmoother do the same for unevenly spaced points. In this case, the delegate takes two vector arguments: the x values and the signal.
Using a smoother delegate does not offer performance advantages over using the direct methods.
In the next example, we use the LOWESS and LOESS filters to smooth the signal.
var yLowess = Smoothing.Lowess(y, windowLength, 0);
var loessSmoother = Smoothing.LoessSmoother(windowLength, 5);
var yLoess = loessSmoother(y);The results are shown below. The derivative is still quite noisy, but also clearly shows the cosine shape we would expect.