Predefined Nonlinear Curves

Defining a nonlinear curve and calculating the partial derivatives can get quite complicated. For this reason, Numerics.NET provides a series of predefined nonlinear curves. Each class implements the ValueAt, ValueAt, and FillPartialDerivatives methods.

The table below lists the predefined non-linear curve types:

These classes reside in the Extreme.Mathematics.Curves.Nonlinear namespace. A more detailed description of each curve type is given below. In the formulas, a parameter a_i represents the parameter with index i in the curve's Parameters collection. For some curves, the individual parameters have a specific meaning, and the class implementing the curve has properties with descriptive names for these parameters. These properties are also listed where available.

An exponential curve is a curve that involves one or more exponential functions e^ax. There is immense variety in the exact definition of different exponential curves. The ExponentialCurve class represents a curve that is the sum of one or more exponential terms:

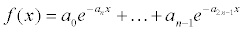
The constructor takes one integer parameter that specifies the number of terms in the curve. The curve has 2n parameters, where n is the number of terms.

A logistic curve is commonly used to represent growth processes.

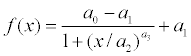
A logistic curve is implemented by the FourParameterLogisticCurve class and has four parameters:

The four-parameter logistic curve is symmetrical in that the change from the initial value and the change towards the final value occur at roughly the same rate. When the data is not symmetrical in this way, the fitted curve may not be a good fit. The five-parameter logistic curve adds an asymmetry parameter that remedies this situation.

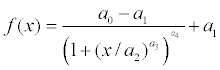
The 5 parameter logistic curve is implemented by the FiveParameterLogisticCurve class and has five parameters:

A Gaussian curve is one type of curve that is used to represent functions with a peak shape:

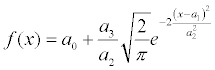
A Gaussian curve is implemented by the GaussianCurve class and takes four arguments:

In addition, the GaussianCurve class has an Amplitude property that returns the difference between the function value at the peak and the baseline (Offset).

A Lorentz curve is used to represent functions with a peak shape. The peak is sharper than the Gaussian curve.

A Lorentz curve is implemented by the LorentzCurve class and takes four arguments:

In addition, the LorentzCurve class has an Amplitude property that returns the difference between the function value at the peak and the baseline (Offset).

A rational curve is a curve that is the quotient of two polynomials. Multiplying both polynomials by a constant gives the same curve. To resolve this ambiguity, the constant term of the polynomial in the denominator is set to 1. A rational curve therefore has n+d+1 parameters, where n is the degree of the polynomial in the numerator, and d is the degree of the polynomial in the denominator:

The RationalCurve class implements this type of curve. The constructor takes two integer parameters: the degree of the polynomial in the numerator, and the degree of the polynomial in the denominator.

A sine curve represents a periodic function.

A sine curve is implemented by the SineCurve class and takes four arguments: