Multivariate Normal Distribution

The multivariate normal distribution is a generalization of the normal distribution. It is characterized by a vector of means μ and a variance-covariance matrix Σ, which must be positive definite. The probability density function is:

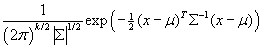
where μ is the vector of means and Σ is the variance-covariance matrix. The multivariate normal distribution is also known as the multivariate Gaussian distribution.

The multivariate normal distribution is implemented by the MultivariateNormalDistribution class. It has two constructors. The first constructor takes two arguments. The first argument is a vector containing the means. The second argumentis a symmetric matrix that contains the covariance matrix.

The following constructs the trivariate normal distribution:

var mu = Vector.Create(3.0, 7.0, 5.0);
var sigma = Matrix.CreateSymmetric(3,
    new double[] { 1.0, 0.3, 0.7, 0.3, 3.0, 1.2, 0.7, 1.2, 5 },
    MatrixTriangle.Upper, MatrixElementOrder.RowMajor);
var mnormal = new MultivariateNormalDistribution(mu, sigma);

Dim mu = Vector.Create(3.0, 7.0, 5.0)
Dim sigma = Matrix.CreateSymmetric(3,
    New Double() { 1.0, 0.3, 0.7, 0.3, 3.0, 1.2, 0.7, 1.2, 5 },
    MatrixTriangle.Upper, MatrixElementOrder.RowMajor)
Dim mnormal = New MultivariateNormalDistribution(mu, sigma)

No code example is currently available or this language may not be supported.

let mu = Vector.Create(3.0, 7.0, 5.0)
let sigma = 
    Matrix.CreateSymmetric(3,
        [| 1.0; 0.3; 0.7; 0.3; 3.0; 1.2; 0.7; 1.2; 5.0 |],
        MatrixTriangle.Upper, MatrixElementOrder.RowMajor)
let mnormal = MultivariateNormalDistribution(mu, sigma)

The two remaining constructors estimate the distribution parameters from a set of variables. One constructor takes a Vector<T> array. The other takes a Matrix<T> whose columns contain the variables.

The GetMeans method returns a Vector<T> that contains the mean of the distribution. The GetVarianceCovarianceMatrix method returns a SymmetricMatrix<T> that contains the variance-covariance matrix of the distribution.

There are two options to generate random samples from the distribution. One is to use the Sample or the Sample method. Sample takes a System.Random and returns a vector with a single sample from the distribution. Sample takes an additional parameter: an integer that specifies the number of samples to return. This method returns a Matrix<T> whose rows contain samples from the distibution. There are also FillSample and FillSamples methods, which copy the sample(s) into the vector or matrix that is supplied as an additional parameter. The example below shows how to generate random samples using each of these techniques:

Pcg32 random = new Pcg32();
var sample = mnormal.Sample(random);
var samples = mnormal.Sample(random, 10000);
mnormal.FillSample(random, sample);
mnormal.FillSamples(random, samples);

Dim random = New Pcg32()
Dim sample = mnormal.Sample(random)
Dim samples = mnormal.Sample(random, 10000)
mnormal.FillSample(random, sample)
mnormal.FillSamples(random, samples)

No code example is currently available or this language may not be supported.

let random = Pcg32()
let sample = mnormal.Sample(random)
let samples = mnormal.Sample(random, 10000)
mnormal.FillSample(random, sample)
mnormal.FillSamples(random, samples)