Kernel Density Estimation
Kernel density estimation (KDE) is a method for estimating the probability density function of a variable. The estimated distribution is taken to be the sum of appropriately scaled and positioned kernels. The bandwidth specifies how far out each observation affects the density estimate.
Kernel density estimation is implemented by the KernelDensity class.
In the code examples, we will repeatedly use a sample generated from a mixture of two Gaussian distributions:
var norm1 = new NormalDistribution(-1, 1);
var norm2 = new NormalDistribution(1, 0.3);
var X = Vector.Join(norm1.Sample(400), norm2.Sample(100));Kernels
A kernel is a non-negative function with mean 0 and area 1. Kernels are implemented by the Kernel class. The KernelDensity class provides several fields that represent common kernels. The available kernels are listed below:
Field | Equation | Chart |
|---|---|---|
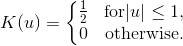 | ||
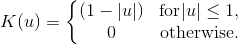 | ||
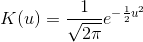 | ||
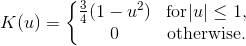 | ||
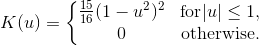 | ||
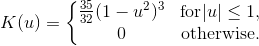 | ||
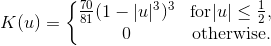 | ||
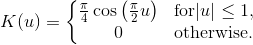 | ||
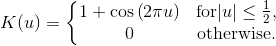 | ||
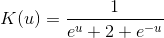 |
Bandwidth
The bandwidth is a parameter in the kernel density estimation that indicates how far the influence of each observation reaches in the density estimate. It is important to get a good value. When the bandwidth is too large, some important features of the true density may be missed. If the bandwidth is too small, the estimated density will be very noisy.
The bandwidth can be supplied directly to the kernel estimation method, or it can be estimated automatically. Three methods are available, enumerated by the KernelDensityBandwidthEstimator enumeration:
Value | Description |
|---|---|
NormalReference | The bandwidth is chosen so it minimizes the integrated square error for normal data. |
Silverman | Use Silverman's rule of thumb. |
Scott | Use Scott's rule of thumb. |
The EstimateBandwidth(Vector<Double>, Kernel, KernelDensityBandwidthEstimator) method returns an estimate of the bandwidth for the specified input. It takes three arguments. The first is a Vector<T> that specifies the data on which the density estimate will be based. The second argument is the kernel. The third argument is a KernelDensityBandwidthEstimator value that specifies the estimation method.
Methods exist that estimate the bandwidth for each of the three techniques. The KernelDensity class has several methods that allow you to estimate the bandwidth. The SilvermanBandwidth(Vector<Double>) and ScottBandwidth(Vector<Double>) methods return the bandwidth using Silverman's and Scott's rule of thumb, respectively. These methods take one argument: a Vector<T> that specifies the data on which the density estimate will be based. The NormalReferenceBandwidth(Vector<Double>, Kernel) method returns the normal reference bandwidth. It takes two arguments: a Vector<T> that specifies the data on which the density estimate will be based, and the kernel.
In the code below, we compute the normal reference bandwidth for our sample for a Gaussian kernel. We also compute the bandwidth using Silverman's rule of thumb:
var bwRef = KernelDensity.NormalReferenceBandwidth(X, KernelDensity.GaussianKernel);
var bwSilverman = KernelDensity.EstimateBandwidth(X, KernelDensity.GaussianKernel,
KernelDensityBandwidthEstimator.Silverman);Computing Kernel Density Estimates
The Estimate method computes the estimated density for one value or a range of values. This method takes up to 5 arguments. The first is a Vector<T> that contains the observations for which the density is to be estimated. The second argument is the kernel. The third argument is the value at which to evaluate the density. If a scalar is supplied, then the density at this value is returned. If a vector is supplied, then a vector of the densities at each value of the vector is returned.
The remaining arguments are all optional. The fourth argument is the bandwidth. If omitted, the bandwidth is estimated using the method specified by the KernelDensityBandwidthEstimator value passed as the fifth argument. The default is to use the normal reference bandwidth. The final argument is an adjustment factor for the bandwidth. This is useful when you want to specify the bandwidth as a fraction of an estimated bandwidth. Both these arguments are ignored if the bandwidth was provided explicitly.
In the next example, we compute three different kernel density estimates. First, we use a Gaussian kernel and use the Silverman bandwidth we found earlier. Then we use an Epanechnikov kernel using Scott's rule to get the bandwidth. Finally, we use a tri-weight kernel and for the bandwidth we use half the normal reference bandwidth:
var density1 = KernelDensity.Estimate(X, KernelDensity.GaussianKernel, bwSilverman);
var density2 = KernelDensity.Estimate(X, KernelDensity.EpanechnikovKernel,
bandwidthEstimator: KernelDensityBandwidthEstimator.Scott);
var density3 = KernelDensity.Estimate(X, KernelDensity.TriweightKernel,
bandwidthAdjustment: 0.5);The EstimateDistribution method performs the same operation, but returns a ContinuousDistribution whose probability density function (PDF) is equal to the estimated density. The arguments to this method are mostly the same as before. The first argument is once again a vector of observations. The second argument is the kernel. The third through fifth arguments concern the bandwidth: the explicit bandwidth, the estimation method, and the adjustment, respectively.
The sixth argument specifies the number of points to use in the approximation of the density. If omitted, the smaller of 200 and the number of inputs is used. The seventh argument specifies how far past the lowest and highest observation the approximation should be computed, in units of the bandwidth. The default is 3.
In our last example, we estimate the density of our sample using a Gaussian kernel. The estimate is returned as a probability distribution, which we can then use for other purposes, such as drawing more samples and computing expectation values:
var dist1 = KernelDensity.EstimateDistribution(X, KernelDensity.GaussianKernel);
var moreSamples = dist1.Sample(100);
var expectionValue = dist1.GetExpectationValue(x => Math.Exp(x));